Always rework my examples on your own BEFORE attempting the homework.

Also see the examples Newton–Gregory Interpolating Polynomials. It contains Example 1 (worked in class). YOU SHOULD WORK EXAMPLE 2 YOURSELF.
However, this document does NOT cover all the details I discussed in class! So if you missed class, you should work all of Example 2 and obtain the lecture notes from a classmate to check your steps.

1. Work Example 2 in the lecture notes on your own. Here are the answers you should obtain.

2. Construct the difference table for the following data from Gerald and Wheatley:

   

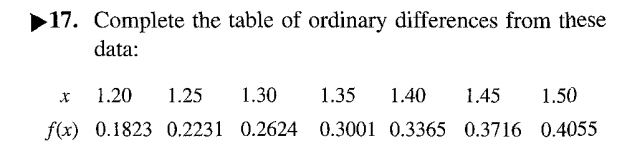
   1. Construct the Newton–Gregory interpolating polynomial that contains the 3rd, 4th, 5th, & 6th points. Use it to estimate f (1.37). Use the telescopic property to compute the binomial coefficients.
      Answer:   f (1.37) ≈ 0.314816000
      

   2. What is the interval of interpolation for the polynomial in Part (a)?
      Answer:   [1.30, 1.45]   or   1.30 ≤ x ≤ 1.45

   3. Use the "next term rule" to estimate the interpolation error in Part (a).
      Answer:   Error  ≈  +0.00000224

   4. Estimate the error in Part (a) in parts per million.
      Answer:   Error  ≈  7.11 ppm

3. Suppose we construct the polynomial through points labeled 0, 1, 2, & 3.
   1. What degree polynomial do we expect to obtain?
   2. What degree is the polynomial if  Δ³f₀  =  0?
      What does that say about the 4 points?

4. Suppose we construct the polynomial through points labeled 2, 3, 4, 5, & 6.
   1. What degree polynomial do we expect to obtain?
   2. What degree is the polynomial if   Δ⁴f₂  =  0?
      What does that say about the 5 points?
   3. What degree is the polynomial if   Δ³f₂  =  0   and   Δ⁴f₂  =  0?
      What does that say about the 5 points?

5. Refer again to the data in Problem 2. Using x = 1.30 as the first abscissa, approximate
   f(1.33) by a 3rd degree polynomial. Use the telescopic property to compute the binomial coefficients. Also estimate the interpolation error.
   Answers:   f (1.33)  ≈  0.2851760
   Error   ≈   – 0.0000033600
   • Estimate the error in parts per million.
     Answer:   Error   ≈  − 11.8 ppm

6. Use the following data from Gerald and Wheatley to answer the stated questions..

   
   

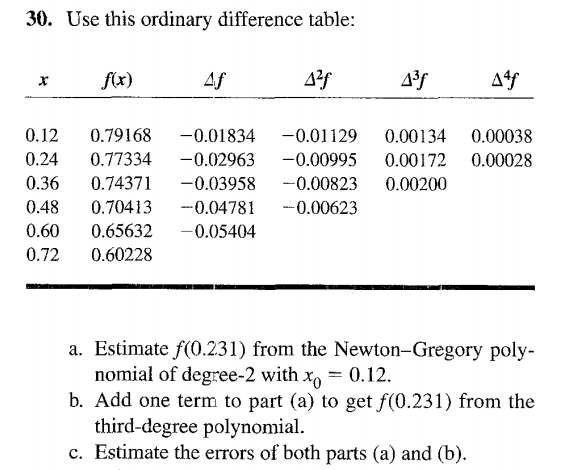
   Answers:

   1.  0.77510 71218 75000    Error  ≈  0.00001 66557 81250    or    0.214 permyriad
   2.  0.77512 37776 56250    Error  ≈  − 0.00000 24502 02148    or    − 3.16 ppm

7. To appreciate the efficiency of the Newton–Gregory method, see these examples that demonstrate
   the amount of work that would be involved IF we were to use brute force algebra instead.

Return to main index