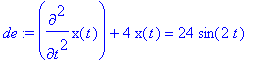
Dr. Kevin G. TeBeest
Assoc. Prof. of Applied Mathematics
Kettering University

RLC Example 4:   Pure Resonance

> restart;de:= diff(x(t),t$2) + 4*x(t) = 24*sin(2*t);

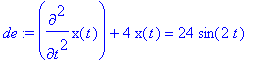
Solve the above ODE, subject to zero initial position and zero initial velocity. Store the result in X:

> X:= rhs( dsolve( {de, x(0)=0, D(x)(0)=0 }, x(t) ) );

Simplify the solution, and store the result in X:

> X:= combine( X, trig );

Plot the solution:

> plot( X, t=0..15, q=-100..100, title=`RLC Example 4: Pure Resonance`, ytickmarks=3,thickness=5,titlefont=[HELVETICA,BOLD,14],labelfont=[TIMES,ITALIC,14]);