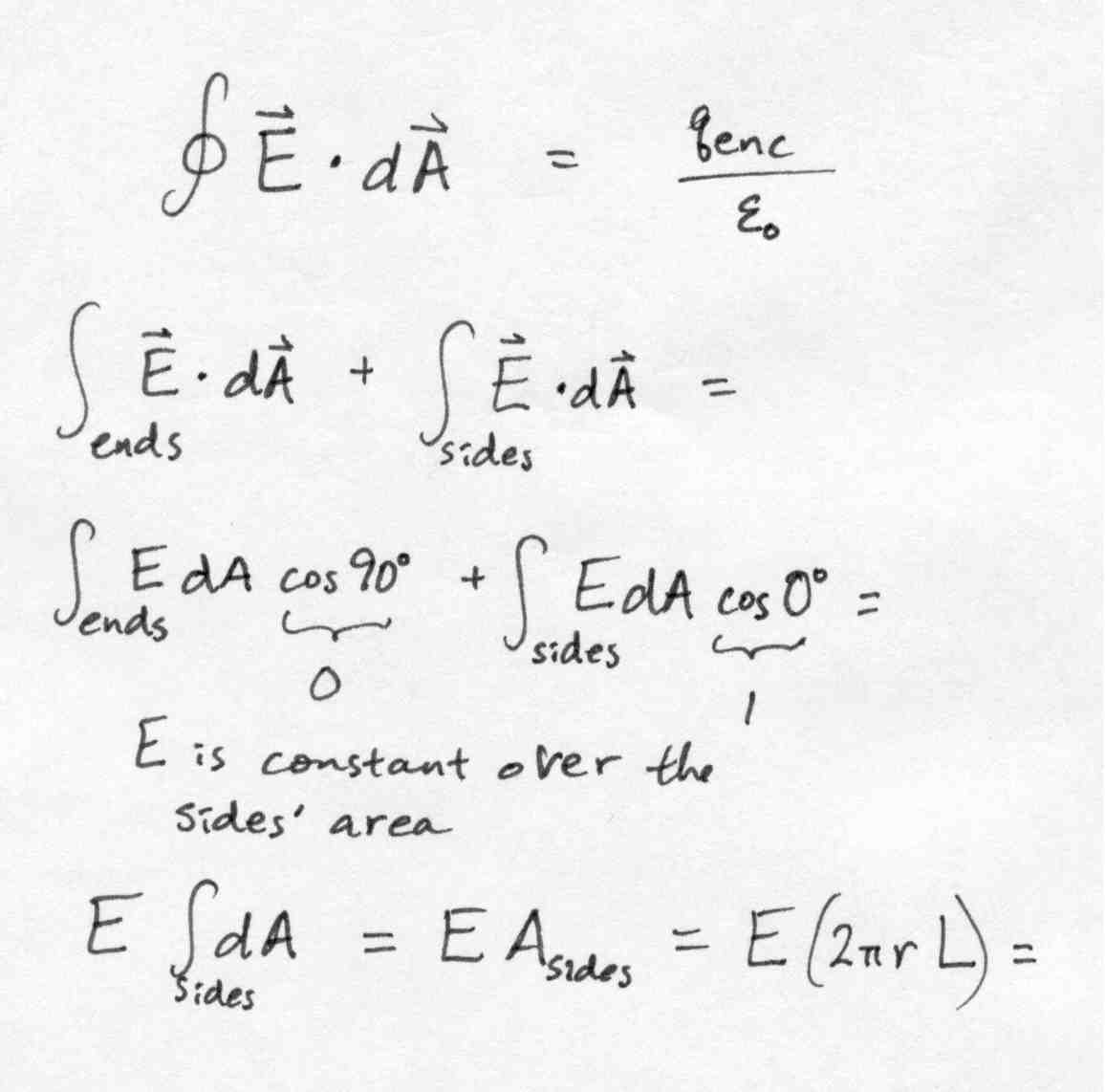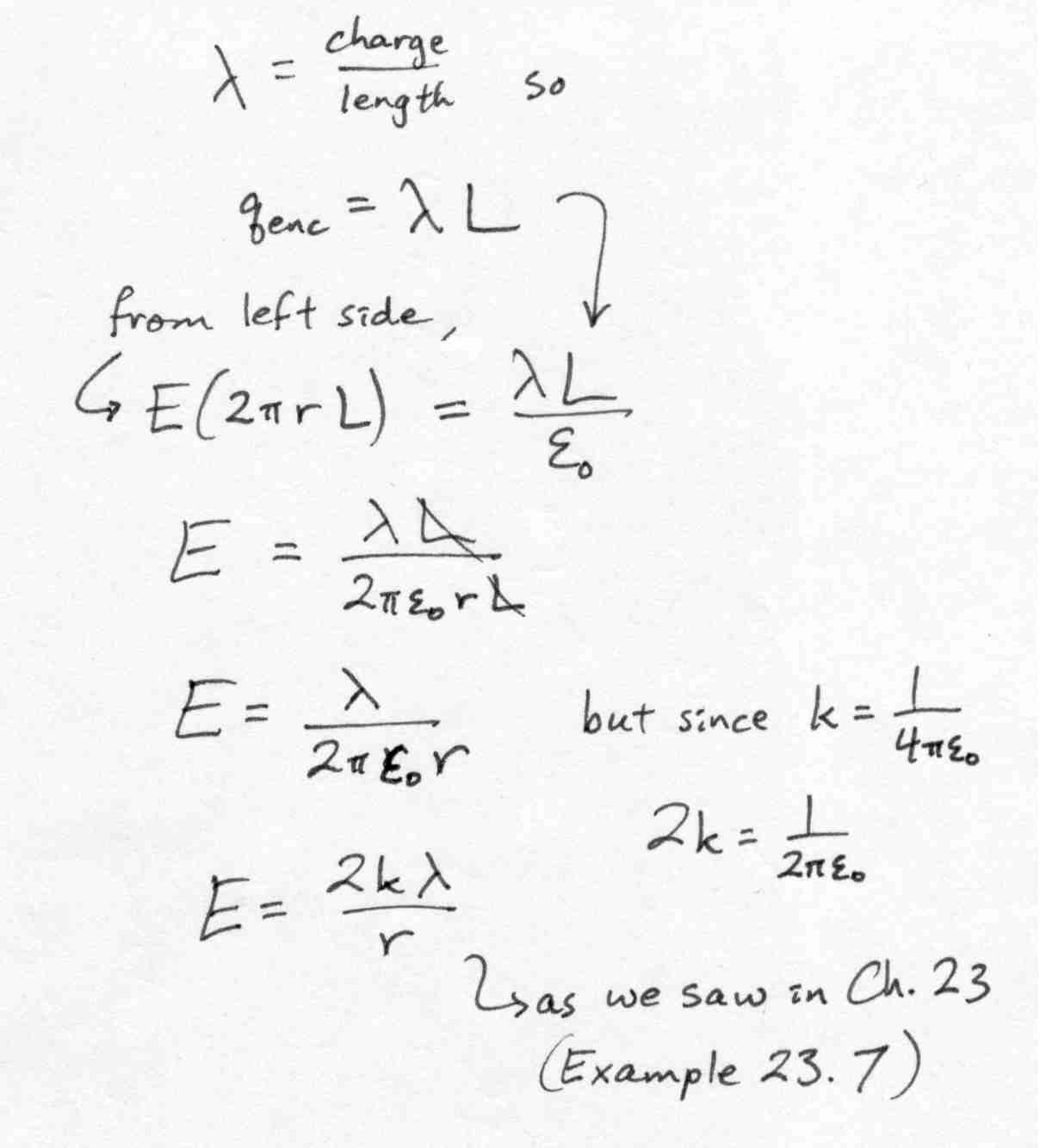Physics 224 - Electricity and Magnetism - Study Guide v 2.0

Written and developed by Dan Ludwigsen for Kettering University - Applied Physics.
These questions and solutions are not guaranteed to be accurate, but are only intended to be helpful.
You are welcome to send comments and questions to dludwigs@kettering.edu.
The last update of this material was on or about April 5th, 2002.

Gauss' Law

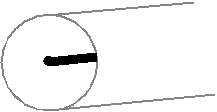
2.1 Consider this model of a coaxial cable: Let the signal wire be a line charge with positive charge per unit length (+lambda). Let the shield be a cylindrical shell (that is, a hollow tube with infinitely thin walls) carrying negative charge per unit length (-lambda) with a radius of a = 5.00 mm. Find the electric field (as a function of the radial distance r) for r<a and r>a.

Did you get

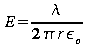for r<a, and E = 0 for r>a?

2.1a Attack the field inside first. To find the field inside the cylindrical shell (r < a), draw a Gaussian surface there. You'll want to take advantage of the symmetry of the charge distributions, so make it a cylinder with its axis along the line charge. Sketch this on your paper - be sure to label the details! Don't forget you'll need to have endcaps to make it a closed Gaussian surface.

My sketch:

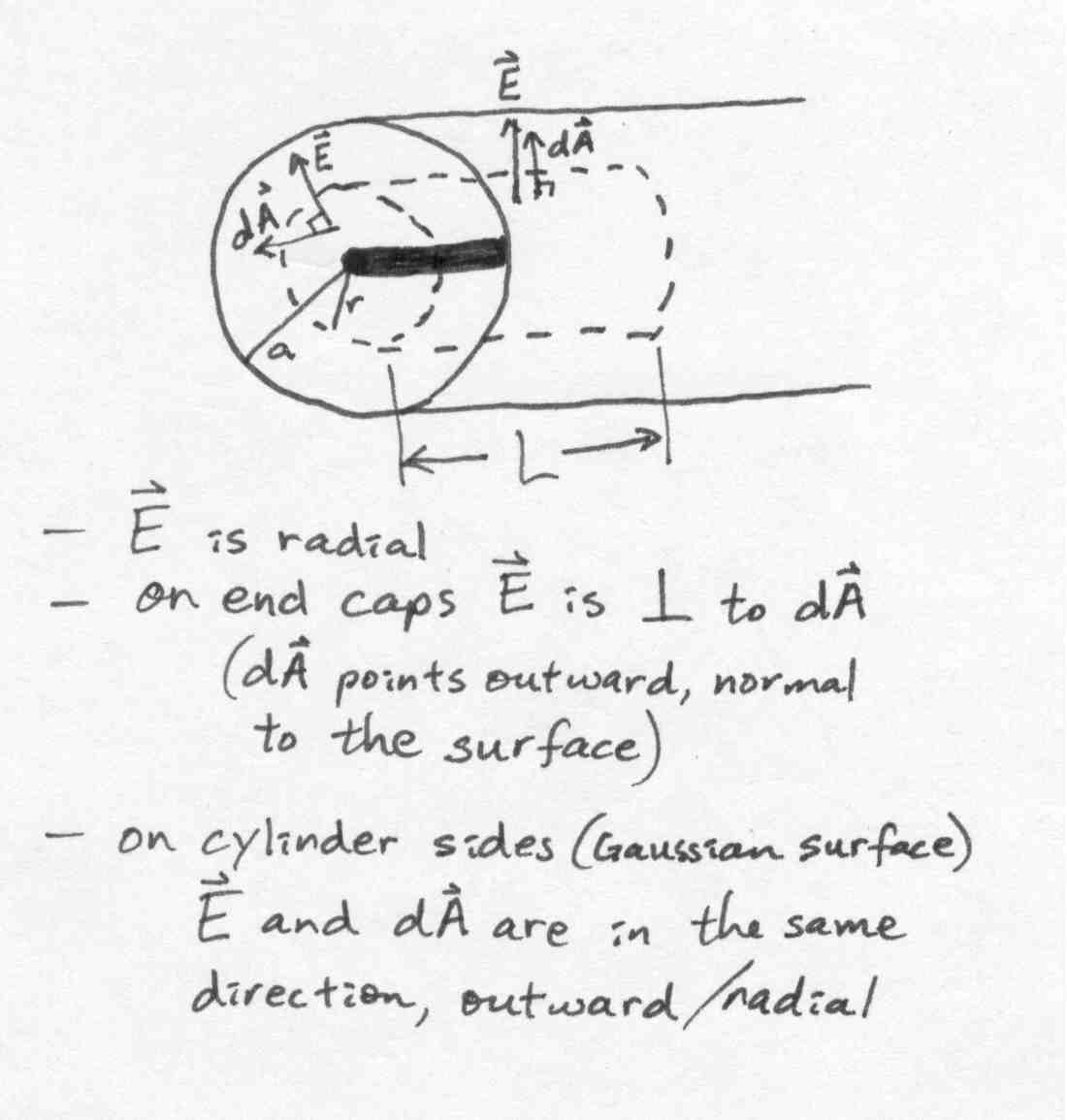
Go to part 2.1b...

2.1b Check for your symmetry advantages with the surface you drew:

write Gauss' Law
evaluate the dot product in the integral on the left side

check both the sides and the ends, since you are integrating over the entire closed surface
split the integral into separate terms to make it clear that you treat the sides differently than the ends

now that the vectors are gone, look at the variables inside the integrals -- are any constant over the area integrals?

if E is constant, pull it out of the integral
if cos(theta) is present and it's constant, pull it out of the integral

work the integral (with symmetry advantages, usually all that is left is the integral of dA)
simplify the left side of the equation until you are satisfied

My version:

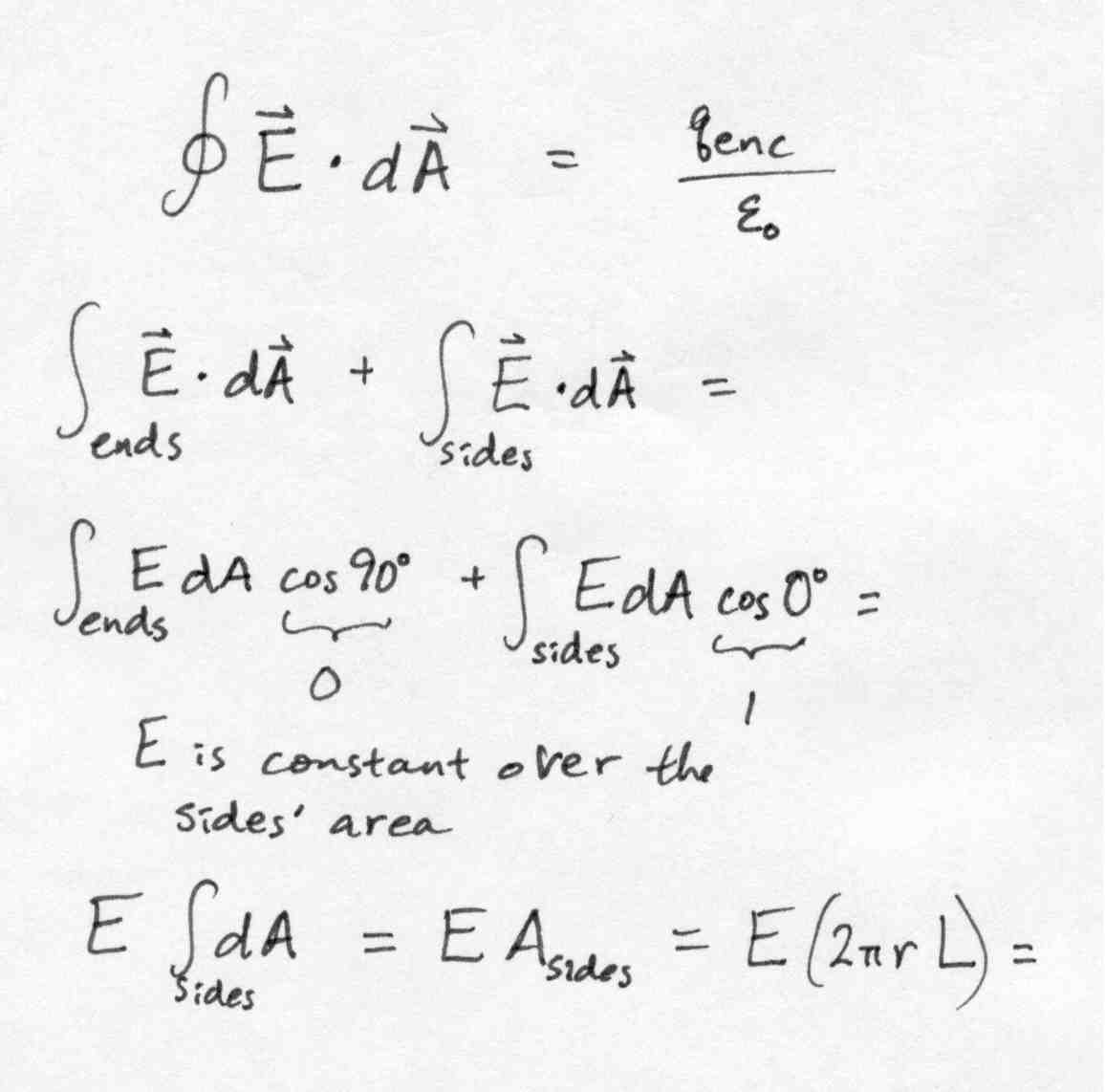
Go to part 2.1c to work the right side and finish up, if you need assistance.
Otherwise go to 2.1d to find the field outside the cylinder.

2.1c The right side of the equation is the charge enclosed by the Gaussian surface divided by a constant, the permittivity of free space.

So first we must figure out how much charge is enclosed by the Gaussian surface. The Gaussian surface is a cylinder -- a product of our design --around it. That imagined Gaussian cylinder encloses some length of the line charge within. Use the definition of linear charge density to solve for the charge enclosed by the Gaussian cylinder. Then put it all together: left side equals right side, then solve for E.

The way I worked it:

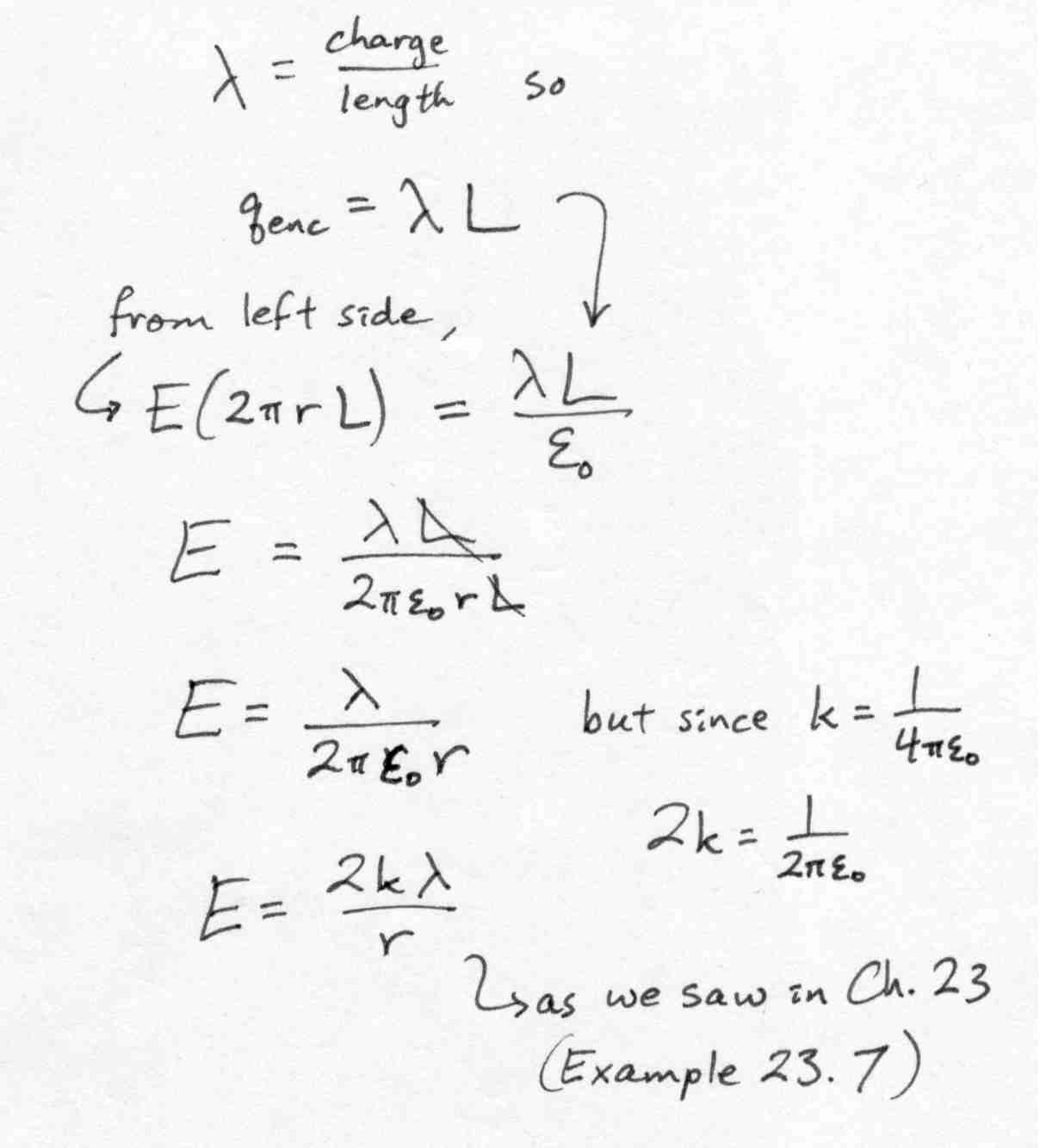
Go to 2.1d to find the field outside the cylinder.

2.1d Now repeat the process for a Gaussian cylinder enclosing both the line charge and the shell. Make the radius greater than a, in other words. Be careful about the net charge enclosed, and be sure to consider symmetry arguments.

My reasoning and calculations:

Now go to the text and try working exercise 24.17.