Brian McCartin, professor of Applied Mathematics at Kettering, has solved a 100-year old problem of linear regression, and his mathematics are "pretty." Linear regression, simply put, means the "best straight line to correlate to the data in question," said McCartin. The problem that he solved was to find this line using simple geometry rather than complicated formulas.

This regression line is used primarily in the fields of Engineering and Science to determine numerical values for physical parameters such as spring stiffness in automotive engineering and electrical resistance, according to McCartin.

The problem first arose in 1886 when Sir Francis Galton, discoverer of modern fingerprinting techniques and first cousin of Charles Darwin, provided a geometrical solution in which only one variable in experimental data is in error. Karl Pearson, one of the founding fathers of modern Statistics, added to the evolution of the solution in 1901 when he developed a geometrical solution in which both variables were in error, but with equal variances (spread of the data).

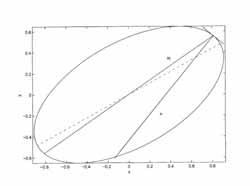
McCartin closed the loop in 2001, by extending this geometrical solution to include unequal variances in the data. And he did it the old fashioned way. "The math tools I used were not from the 20th Century," said McCartin, "I went back to the Third Century. The math I used you could explain to the average high school student." The tools he used were the ancient Greek geometry of the ellipse (paths of planets around the sun attributed to Appolonius of Perga, Third Century B.C.) and the Concentration Ellipse from the field of statistics. Statistics is a branch of Applied Mathematics widely used by the insurance industry as well as by engineers, according to McCartin.

His "pretty math," refers to what McCartin calls the Mathematician's Credo "There is no place in the world for ugly Mathematics." In other words, a geometrical problem should have a geometrical solution, not just a messy formula for an answer. "Rather than derive a complicated formula, a simpler pictorial solution is the desired outcome," said McCartin, " and it's prettier."

McCartin's pretty solution to the geometry of linear regression came about by accident. "It just popped out as an interesting byproduct of a project I was working on with Dr. Pat Atkinson regarding knee replacement surgery," said McCartin. Atkinson, assistant professor of Mechanical Engineering at Kettering, had asked McCartin to do some statistical work on data collected for a bio-mechanical engineering research project. "I enjoy working with engineers, they bring me interesting problems to solve so that I can be useful," said McCartin.

Professor McCartin's solution has been accepted for publication in the prestigious "Statistics" Journal.

"The double irony is that I am not a statistician, I study differential equations. I just stumbled onto to this solution," McCartin said. According to McCartin, many mathematical problems are solved communally. "Over time a lot of people will peck away at a problem, but when you get to throw the final blow, it's lots of fun," he said.

McCartin's solution has been accepted for publication in the prestigious "Statistics" Journal. "It's a feather in my cap professionally," he said. Other than that, his reward will be to have his name added to that of Galton and Pearson in the mathematical history of linear regression.

Originally from Providence, R.I., McCartin received his bachelor's and master's degrees from the University of Rhode Island and his doctoral degree in Applied Mathematics from the Courant Institute of Mathematical Sciences at New York University. He is immediate past-vice president of the Great Lakes Section of the Society for Industrial and Applied Mathematics, and winner of the Kettering 2000 Outstanding Researcher Award and 2001 Outstanding Teacher Award.

Written by Dawn Hibbard
(810) 762-9865
dhibbard@kettering.edu
Used with permission.