Example: A Bessel Function & Partial Sums

Dr. K.G. TeBeest

This is Example 3 on page 742. Furthermore, we studied partial sums in Section 11.2.

In Maple, the Bessel function (of order 0) is BesselJ(0,x) .

The series representation of the Bessel function (of order 0) is

Set the term in the Bessel function's series as a function of n:

> a := n -> (-1)^n * x^(2*n) / ( 2^(2*n) * (n!)^2 ) ;

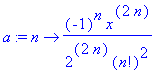
Construct the N th partial sum (add all terms up to term N ) as a function of N:

> s := N -> sum( a(n), n = 0 .. N ) ;

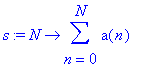
See the 2nd, 3rd, and 4th partial sums:

> s(2) ;

> s(3) ;

> s(4) ;

Plot the Bessel function on the interval [ -8, 8 ]:

> plot( BesselJ( 0, x ), x = -8 .. 8, -1 .. 1, thickness = 4 ) ;

Plot the Bessel function along with the partial sums on the interval [ -8, 8 ]:

s(2)- red , s(3)- yellow , s(4)- pink , s(5)- green . The Bessel function is in blue.

Note that as we keep more terms in the series, the partial sums (red, yellow, pink, green) give better approximations to the Bessel function (blue).

> plot( { s(2), s(3), s(4), s(5), BesselJ(0,x) }, x = -8 .. 8, -1 .. 1, thickness = 4 ) ;